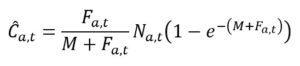FOCUS technique : dynamique des populations

1. Contexte

• 1.1 Définition et historique

La dynamique des populations correspond à la discipline dont le but est d’étudier l’évolution démographique, autrement dit les fluctuations dans le temps de l’effectif des populations au travers différents modèles mathématiques. Les premiers travaux visant à décrire les variations temporelles du nombre d’individus sont le fruit de Fibonacci (1170-1250) qui, en voulant décrire le nombre de lapins qu’aurait un homme en un an en ne possédant qu’un couple au début de l’année, a ainsi décrit le premier modèle pouvant être considéré comme de la dynamique des populations (Bacaër 2011). Euler (1707-1783) a ensuite imagé certains de ses travaux mathématiques sur l’exponentielle et les logarithmes dans Introduction to Analysis of the Infinite en utilisant des exemples de populations avec des variations d’effectifs (Bacaër 2011). Alors que Bernoulli (1700-1782) utilisa certains modèles pour estimer la mortalité due à la variole et l’effet de la vaccination dessus, l’essor véritable de la dynamique des populations en tant que discipline est le fruit de Malthus, mathématicien anglais (1766-1834) qui travailla sur la croissance d’une population et montra qu’une population augmente de manière géométrique (exponentielle) si les ressources ne manquent pas.

Une grande avancée fut celle de Verhulst (1804-1849) qui démontra la croissance logistique pour une population, croissance qui diminue dès lors qu’un certain effectif est atteint. C’est à partir de ses travaux, qu’un terme de son modèle sera ensuite nommé capacité de charge du milieu ou carrying capacity en anglais. Dans la lignée des travaux de Malthus et Verhulst, Gompertz (1779-1865) retravailla et développa le modèle de Malthus pour prendre en considération que la mortalité dépend de l’âge des individus. Plus tard, ce modèle sera complété par Makeham pour former le modèle de Gompertz-Makeham dans lequel la mortalité dépend d’un terme relié à l’âge (fonction de Gompertz) et d’un terme indépendant de l’âge (fonction de Makeham). Alors que les travaux de Verhulst, Gompertz, Malthus, ou Bernoulli étaient centrés sur des populations humaines, un des modèles de dynamique des populations les plus connus est celui de Lotka-Volterra. Leur modèle a cherché à comprendre et modéliser la dynamique d’une population de lynx et d’une population de lièvre ; l’un étant le prédateur, l’autre la proie. Ce modèle a ensuite servi de base aux études décrivant les dynamiques de systèmes proies-prédateurs.

• 1.2 Généralités et philosophie des modèles

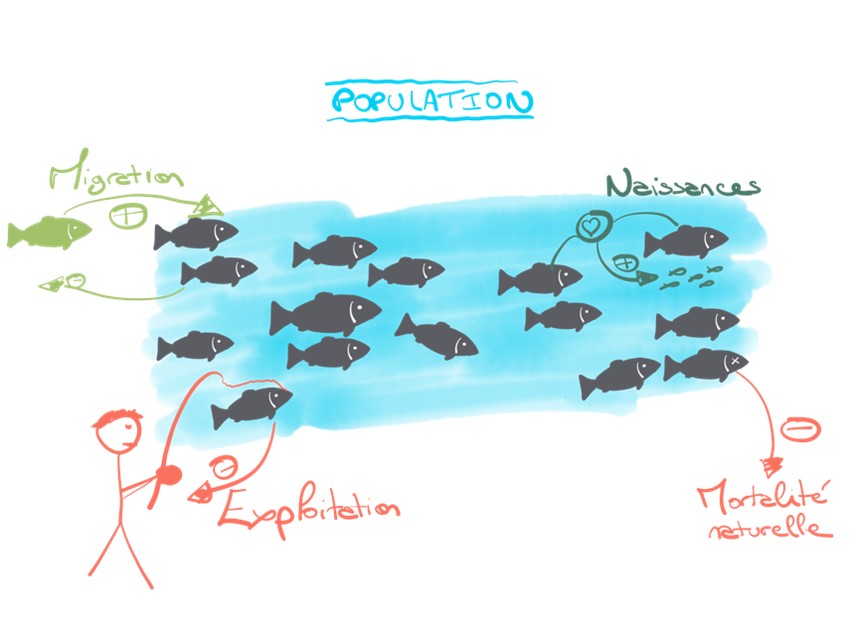
Aujourd’hui, la majeure partie des modèles de dynamique de populations sont construits autour de plusieurs termes. Si on considère Nt comme étant le nombre d’individus d’une population à l’instant t , alors à l’instant d’après t + 1 , le nombre d’individus est donné par : Nt + 1 = Nt + B – M – E + I. Dans cette équation, les différents termes représentent le nombre de naissances B, le nombre de morts M, le nombre d’immigrés I, le nombre d’émigrants E. Les différents modèles vont chercher à définir chacun des termes en fonctions des espèces, populations, contextes de celles-ci, …. Par exemple, les deux derniers termes E et I vont dépendre de si la population est isolée ou non ; et si elle n’est pas isolée il sera alors important d’estimer les échanges avec les autres populations. Les modèles cherchant à expliquer les variations d’abondance de populations en interaction vont donc s’intéresser soit aux interactions entre deux ou plusieurs espèces (modèles proies-prédateurs de type Lotka-Volterra) ou aux interactions entre populations d’une même espèce via les termes E et I notamment. Ce type d’études est notamment pertinent dans le cadre des méta-populations correspondant à des populations reliées les unes aux autres par des échanges d’individus.

Dans le cadre des populations isolées pour lesquels les termes E et I sont nuls, la croissance de la population ne repose alors que sur les termes B et M. Cette croissance peut être linéaire, géométrique (exponentielle), ou logistique. Alors que les croissances linéaires et géométriques reposent sur des ressources non-limitantes, la croissance logistique repose sur la densité-dépendance. Celle-ci peut être positive, on parle alors de densité-dépendance dépensatoire (ou depensatory density-dependence), quand la survie des individus augmente avec l’abondance. À l’inverse, elle peut être négative dès lors que la survie des individus diminue lorsque l’abondance augmente, on parle alors de densité-dépendance compensatoire. La densité-dépendance négative est la plus courante dans les modèles naturels. Ainsi, des ressources limitantes peuvent conduire à de la compétition entre individus et donc une sur-mortalité, ou une difficulté pour les individus à se trouver lors de la reproduction (effet Allee).

schéma des processus démographiques dans une population piscicole exploitée.

Dans la majorité des cas d’études, les populations sont dites structurées. C’est à dire que les paramètres d’histoire de vie qui vont affecter la démographie tels que la survie et la fécondité varient avec l’âge ou le stade de vie des individus. Ainsi, il peut donc être primordial et nécessaire de prendre en compte ces variations temporelles et donc la structure de la population dans les modèles de dynamique de population. Par exemple, les femelles saumons ont une fécondité qui varie selon le nombre d’hivers passés en mer tandis que la survie des juvéniles 0+ (nés dans l’année) est souvent inférieure à celle des juvéniles 1+ (nés l’année précédente).

Avoir une bonne connaissance de la population ciblée est donc primordiale pour définir les modèles adéquats. Cette connaissance passe par l’acquisition de données et une revue bibliographique poussée que ce soit sur l’espèce, le territoire, et/ou la population visée pour identifier les processus démographiques pouvant s’appliquer.

2.    Détail de la technique

Voici quelques étapes générales sur la façon dont on réalise l’étude de la dynamique des populations :

• Collecte de données : La première étape consiste à collecter des données sur la population étudiée. Cela inclue généralement un indice d’abondance, la collecte de données démographiques (comme la taille, l’âge, le sexe, la fécondité, la mortalité) et des données environnementales. Étant donné que la dynamique des populations s’intéresse aux évolutions démographiques, il est nécessaire de recueillir des données sur un nombre important d’années.
• Analyse des données : Une fois que les données ont été collectées, elles sont analysées pour identifier les tendances et les fluctuations d’abondance, ainsi que les processus démographiques en jeu dans la population au travers différents modèles tels que les modèles à croissance exponentielle ou logistique, ou bien les modèles matriciels de Leslie prenant en compte la structure de la population.
• Modélisation des populations : À partir des paramètres estimés via l’analyse des données, il est possible de faire des prédictions sur les populations étudiées pour estimer les potentielles évolutions de la population. Cela peut également permettre de faire des projections selon différents scénarios de gestion : amélioration de la survie d’une classe d’âge, changement des processus de migration, …
• Interprétation des résultats : Les informations tirées de l’analyse des données et de la modélisation permettent de comprendre les facteurs qui influencent la dynamique de la population, tels que les facteurs environnementaux, les interactions prédateur-proie, la compétition, les interventions humaines, …. Ce travail d’interprétation se fait en confrontation entre les résultats obtenus pour la population étudiée et la littérature scientifique.
• Recommandations pour la gestion : les résultats obtenus peuvent être utiles pour les gestionnaires, les exploitants, les biologistes, ou tout autre acteur pour élaborer des stratégies de gestion appropriée. Par exemple, cela peut impliquer la mise en place de quotas de chasse, la création de réserves naturelles, la restauration de l’habitat, la régulation des espèces invasives, ….
• Gestion adaptative : si la politique de gestion est bien suivie, ainsi que la collecte de données pertinentes, il est possible d’appliquer une stratégie de gestion adaptative ou les recommandations sont mises à jour selon les résultats obtenus. Pour cela, il est nécessaire de mettre en place des modèles de dynamique de populations robustes.

3.    Intérêt de cette méthode pour les acteurs et cas d’utilisation

• 3.1. Intérêt général

L’intérêt principal de ces outils repose sur la possibilité de réaliser des diagnoses de la démographie des populations. Par exemple, les différents modèles peuvent permettre de mettre en évidence une mortalité (terme M) supérieure aux naissances (terme B) ou une survie dépendante de la densité d’individus. Aussi, la modélisation des termes liés à la migration (E et I) peut être pertinente pour des questions de fragmentations de milieu. Concrètement, pour les gestionnaires ces outils statistiques peuvent permettre d’avoir une meilleure estimation des effectifs et donc connaitre la taille de la population et ainsi déterminer son statut de conservation et les mesures de conservation pouvant être mises en place. Ces modèles permettent également une estimation des tendances démographiques et une projection de celles-ci, rendant possible une planification à long terme et des tests de scénarios de gestion tels que l’efficacité des programmes de reproduction, la protection d’habitats, la régulation de l’exploitation, …. Enfin, ces outils permettent une meilleure identification des pressions et facteurs impactant les populations et donc de cibler plus efficacement les actions de conservation à entreprendre.

• 3.2. Cas spécifique pour les populations exploitées : pêcheries

Les populations piscicoles représentent un cas particulier pour la dynamique des populations. En effet, beaucoup d’espèces et de populations sont exploitées par la pêche professionnelle et/ou amatrice. Ainsi, depuis des décennies un certain nombre de modèles de dynamique des populations se sont intéressés à ces populations pour prendre en compte l’exploitation de celles-ci. La philosophie de ces modèles est de prendre en compte explicitement cette exploitation dans le terme lié à la mortalité et ainsi estimer un certain nombre d’indicateurs ou points de référence (Prévost and Chaput 2001).

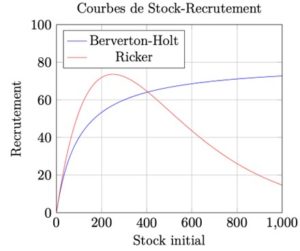
Les premiers modèles sont les modèles dits stock-recrutement qui visent à relier le stock défini par le nombre de géniteurs ou d’œufs, au recrutement souvent défini comme le nombre de juvéniles produits. Les modèles les plus couramment utilisés sont ceux de Berverton-Holt (Beverton and Holt 1957), Ricker (Ricker 1954) et Deriso-Schnute (Schnute 1985). Ces modèles, en permettant de prédire un recrutement pour stock donné, sont utiles pour déterminer le risque pour la population d’avoir un recrutement sous la limite de conservation. De plus, ces modèles font différentes hypothèses sur la densité-dépendance reliant le stock au recrutement ; ajuster ces différents modèles pour identifier celui le plus adapté à la population permet d’identifier les processus démographiques sous-jacents. Bien que ces modèles n’expriment pas directement le processus d’exploitation, ils permettent de définir des points de référence et d’évaluer si le niveau de stock reste supérieur à un seuil déterminé.

Courbes de stock-recrutement de Beverton-Holt et de Ricker

Les modèles de Schaefer et de Baranov vont eux directement identifiés la pression de pêche. Par exemple, le modèle de Baranov est ainsi utilisé pour estimer le taux de capture maximal qui peut être prélevé d’une population de poissons tout en maintenant la durabilité de cette population. Il est basé sur plusieurs hypothèses dont l’existence d’un rendement maximum soutenu (RMS ou MSY en anglais), autrement dit un niveau de capture qui permettrait de prélever le maximum de poissons tout en maintenant la reproduction de manière à maintenir la population à un niveau constant. Les autres hypothèses du modèle sont que le taux de capture du modèle est dépendant de l’effort de pêche et qu’il est proportionnel à la biomasse. Le modèle permet d’estimer le taux de capture maximal durable en fonction de la biomasse de la population et de l’effort de pêche :

4.    Accompagnement proposé par SCIMABIO Interface

SCIMABIO Interface met son expertise au service des acteurs pour transmettre ses connaissances et compétences en lien avec la dynamique des populations. Ainsi, vous pouvez bénéficier de l’expertise scientifique de SCIMABIO Interface pour définir le contexte précis de votre territoire, population d’étude, et identifier les principaux processus démographiques pouvant être impliqués. En s’appuyant sur ses connaissances, SCIMABIO Interface peut également vous aider à identifier les principales interrogations et manquent de connaissances relatives à votre territoire.

L’expertise de SCIMABIO Interface vous permet également de définir et mettre en place un protocole de recueil de données en adéquation avec des analyses démographiques. Les données nécessaires pour des modèles de dynamique des populations sont souvent des indices d’abondance qui doivent être bien définis, récoltés, et ce sur une longue période. Il est en effet difficile d’avoir accès à l’abondance vraie d’une population. On utilise souvent des indices mais dont les variations doivent être proportionnelles aux variations de l’abondance vraie. De plus, il est souvent utile et pertinent d’avoir des données individuelles (taille, poids, fécondité), ainsi que des données environnementales.

SCIMABIO Interface dispose des compétences et connaissances nécessaires et valorisées au sein du Laboratoire Partenarial Associé MODMAF (INRAE / UPPA / SCIMABIO Interface) pour développer et utiliser les modèles de dynamique de population à vos systèmes. En ayant les connaissances scientifiques pour utiliser ces modèles, nous pouvons les ajuster au mieux à vos problématiques et vos populations d’études. Enfin, nos compétences nous permettent de vous proposer des scénarios de gestions, les tester, et produire des évaluations des états des populations, ainsi que des recommandations de gestion. Du fait de l’expertise technique et scientifique, l’accompagnement proposé par SCIMABIO Interface peut être que sur une partie du processus d’analyses ou sur tout le process depuis la revue bibliographique à la production de recommandations de gestion en passant par l’application de modèles spécifiques.

Listes de références publiées par des membres de SCIMABIO Interface

Un certain nombre de travaux réalisés par les collaborateurs de SCIMABIO Interface ont été publiés sur cette thématique dans des revues scientifiques à comité de lecture. Vous en trouverez ici une liste non-exhaustive.

• Bouchard, C., Bardonnet, A., Buoro, M. and Tentelier, C. 2018. Effects of spatial aggregation of nests on population recruitment : the case of a small population of Atlantic salmon. – Ecosphere 9(4).
• Bouchard, C., Buoro, M., Lebot, C. and Carlson, S. M. 2022a. Synchrony in population dyamics of juvenile Atlantic salmon : analyzing spatiotemporal variation and the influence of river flow and demography. – Canadian Journal of Fisheries and Aquatic Sciences 79(5) : 782–794.
• Bouchard, C., Drouineau, H., Lambert, P., Boutron, O. and Nicolas, D. 2022b. Spatio-temporal variations in glass eel recruitment at the entrance pathways of a Mediterranean delta. – ICES Journal of Marine Science 79 : 1874–1887.
• Vallecillo, D., Guillemain, M., Authier, M., Bouchard, C., Cohez, D., Vialet, E., Massez, G. et al. 2022. Accounting for detection probability with overestimation by integrating double monitoring programs over 40 years. – PLOS ONE 17(3) : e0265730.
• Vallecillo, D., Guillemain, M., Bouchard, C., Roques, S. and Champagnon, J. 2023. Influence of changes in local environmental variables on the distribution and abundance dynamics of wintering Teal Anas crecca. – Biodiversity and Conservation.

Références.

Bacaër, Nicolas. 2011. A Short History of Mathematical Population Dynamics. London: Springer London. https://doi.org/10.1007/978-0-85729-115-8.

Beverton, Raymond J. H., and Sidney J. Holt. 1957. On the Dynamics of Exploited Fish Populations. Vol. 19. 2nd Series. Dordrecht: Springer Netherlands. http://link.springer.com/10.1007/978-94-011-2106-4.

Prévost, Etienne, and G Chaput. 2001. Stock, Recruitment and Reference Points: Assessment and Management of Atlantic Salmon. Paris, France: INRA Editions.

Ricker, W. E. 1954. “Stock and Recruitment.” Journal of the Fisheries Research Board of Canada 11 (5): 559–623. https://doi.org/10.1139/f54-039.

Schnute, Jon. 1985. “A General Theory for Analysis of Catch and Effort Data.” Canadian Journal of Fisheries and Aquatic Sciences 42 (3): 414–29. https://doi.org/10.1139/f85-057.