Passer au contenu principal
Focus techniqueActualitésStatistiques Bayésiennes

FOCUS Technique : statistiques Bayésiennes

Par 20 novembre 2023février 1st, 2024Aucun commentaire

Apports des statistiques Bayésiennes dans les analyses de données en écologie appliquée

Contexte

Les statistiques Bayésiennes réfèrent à une approche des statistiques caractérisée par l’utilisation des distributions probabilistes pour décrire une quantité inconnue – par exemple un paramètre d’un modèle. Cette approche prend son nom du théorème sur lequel elle est basée : le théorème de Bayes. Bayes (1702–1761) était un mathématicien du XVIIIème siècle et en s’intéressant à un problème autour des probabilités conditionnelles, il a formulé le résultat mathématique d’un cas particulier du théorème qui porte aujourd’hui son nom. Il voulait utiliser une distribution Binomiale pour représenter r succès parmi n essais pour connaitre la chance sous-jacente et inconnue θ qu’un essai soit un succès. La contribution de Bayes a dont été d’utiliser une distribution probabiliste pour représenter les incertitudes à propos de θ. C’est Laplace – un autre mathématicien (1749–1827) – qui viendra ensuite généraliser le résultat de Bayes pour donner le théorème connu aujourd’hui.

  •  Principe

Le théorème de Bayes est donc basé sur les probabilités conditionnelles. La formule du théorème de Bayes est la suivante :

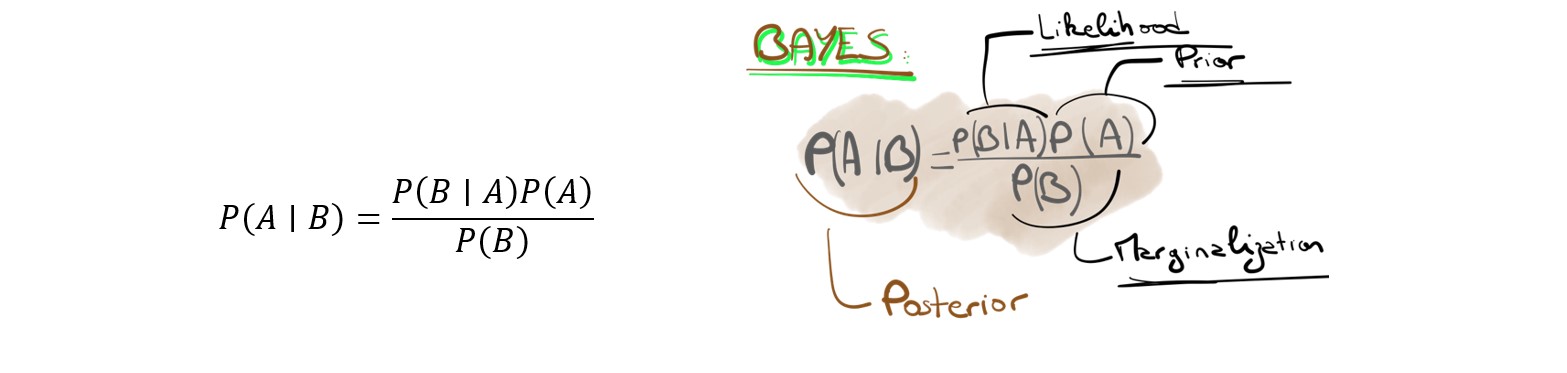
Si on considère A et B comme deux évènements, et que B correspond à des données, tandis que A correspond à une hypothèse (i.e., un paramètre à estimer), alors la formule peut être traduite comme cela :

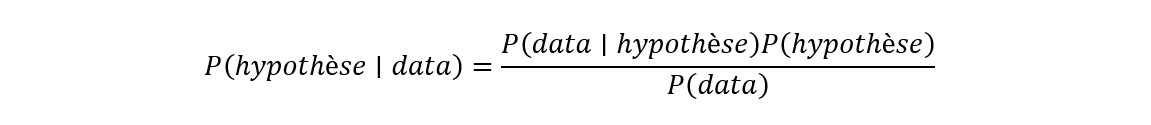
Le théorème permet d’estimer la probabilité de l’hypothèse sachant les données. L’hypothèse est souvent quelque chose qui ne peut être observé. Par exemple, il est impossible de connaitre la taille moyenne d’une population de poissons dans un lac, hormis si on capture l’entièreté des individus, ce qui est peu probable. Bien souvent, la taille moyenne est estimée à partir d’échantillons.

L’approche Bayésienne est donc basée sur l’idée que des connaissances sont disponibles avant l’expérience. Ainsi, ces connaissances sont actualisées à partir des données observées et collectées. Si on note ces connaissances par  alors :

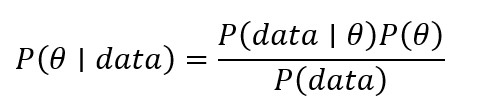
SCIMABIO Interface, statistiques bayesiennes, formule 2

Avec  P(θ)- la distribution a priori – qui représente ce que l’on sait avant d’avoir vu les données. P(data/θ) correspond à la vraisemblance – likelihood – d’obtenir les données à partir des connaissances / paramètres. C’est la même quantité que l’approche par Maximum de Vraisemblance. P(data) correspond à une intégrale ayant autant de dimensions qu’il y a de paramètres θ. Enfin, P(θ/data) correspond à la distribution a posteriori de θ sachant les données observées et les connaissances a priori.

La grande différence des statistiques Bayésiennes par rapport aux statistiques classiques, dites fréquentistes est donc l’apport de connaissances a priori et l’utilisation de distributions probabilistes. Cela se traduit par la lecture des intervalles de confiance. La lecture Bayésienne d’un intervalle de confiance à 95 % d’un paramètre est qu’il y a une probabilité égale à 0,95 que l’intervalle contienne la vraie valeur du paramètre (la valeur inconnue qu’on cherche à estimer). Ainsi, les bornes de l’intervalle bougent mais pas la vraie valeur du paramètre qui nous est inconnue. L’approche fréquentiste voit plutôt les intervalles de confiance comme la résultante d’une multitude d’expérimentation. Pour les Bayésiens, les paramètres sont donc vus comme des variables aléatoires. Ainsi, les paramètres sont vus comme fixes et inconnus pour les Fréquentistes, alors qu’ils sont inconnus et avec une certaine distribution probabiliste pour les Bayésiens.

2.    Avantages et intérêts des statistiques Bayésiennes pour l’écologie

Les statistiques Bayésiennes offrent plusieurs avantages lorsqu’elles sont appliquées à la recherche en écologie :

  • Incorporation de Connaissances Antérieures : Les statistiques Bayésiennes permettent aux écologistes d’inclure des informations déjà connues sur un système dans leurs analyses. Cela est particulièrement utile en écologie, où il existe souvent une connaissance préexistante des relations entre les espèces, les facteurs environnementaux et d’autres variables. En incorporant ces connaissances antérieures, il est possible d’obtenir des inférences plus éclairées et réalistes. Dans l’exemple de la taille moyenne d’une population de poisson, ces informations peuvent provenir d’autres populations de la même espèce par exemple.
  • Petites Tailles d’Échantillon : Les analyses Bayésiennes peuvent fournir des résultats fiables même avec de petites tailles d’échantillon, ce qui peut être courant en écologie en raison de contraintes logistiques et budgétaires. La capacité à incorporer des informations antérieures aide à obtenir des inférences plus fiables avec des données limitées.
  • Estimation des Paramètres : Les statistiques Bayésiennes fournissent une distribution de valeurs de paramètres possibles, au lieu d’une seule estimation ponctuelle comme dans les statistiques fréquentistes. Cette distribution offre une compréhension plus complète de l’incertitude, permettant de faire des interprétations plus nuancées.
  • Flexibilité : Les méthodes Bayésiennes sont flexibles et peuvent gérer des modèles complexes, ce qui est souvent nécessaire en écologie où les systèmes sont intrinsèquement complexes et interconnectés. Cette flexibilité permet aux chercheurs de construire des modèles qui capturent plus précisément les nuances des interactions écologiques.
  • Modèles Hiérarchiques : Les systèmes écologiques impliquent souvent des structures hiérarchiques, comme des données collectées à plusieurs échelles spatiales ou temporelles. Les méthodes bayésiennes sont bien adaptées à la construction de modèles hiérarchiques qui peuvent prendre en compte ces relations complexes.
  • Prédiction et Prise de Décision : Les statistiques Bayésiennes fournissent un cadre pour faire des prédictions basées sur les données disponibles et les informations antérieures. Cela est précieux dans la gestion écologique et la conservation, où les décisions doivent être prises sur la base d’informations incertaines.
  • Prise en Compte de l’Incertitude : Les statistiques Bayésiennes quantifient explicitement l’incertitude à travers des distributions de probabilité. Cela est crucial en écologie, où les données peuvent être bruitées et les mesures sujettes à diverses sources d’erreur.
  • Prise en Compte des Données Manquantes : Les données écologiques peuvent souvent comporter des valeurs manquantes ou des observations incomplètes. Les méthodes Bayésiennes offrent un cadre pour gérer les données manquantes et imputer les valeurs de manière probabiliste.

En résumé, les statistiques Bayésiennes fournissent un cadre puissant et flexible pour analyser les données écologiques, incorporer des connaissances antérieures, traiter l’incertitude et prendre des décisions éclairées dans des écosystèmes complexes et dynamiques.

3.    Accompagnement proposé par SCIMABIO Interface

SCIMABIO Interface met son expertise au service des acteurs pour transmettre ses compétences en lien avec l’utilisation des statistiques Bayésiennes. Ainsi, vous pouvez bénéficier de l’expertise scientifique de SCIMABIO Interface pour analyser vos données existantes ou construire un modèle particulier visant à acquérir une connaissance ciblée et définir le jeu de données (le protocole) nécessaire à mettre en place. L’expertise de SCIMABIO Interface vous permet également de définir et mettre en place un protocole de recueil de données en adéquation avec les modèles construits.

SCIMABIO Interface dispose des compétences et connaissances nécessaires et valorisées au sein du Laboratoire Partenarial Associé MODMAF (INRAE / UPPA / SCIMABIO Interface) pour développer et utiliser ces méthodes à vos systèmes. En ayant les connaissances scientifiques pour utiliser ces méthodes, nous pouvons les ajuster au mieux à vos problématiques et construire des modèles qui permettent de valoriser vos données pour développer les connaissances sur vos systèmes. Du fait de l’expertise technique et scientifique, l’accompagnement proposé par SCIMABIO Interface peut être que sur une partie du processus d’analyses ou sur tout le process depuis la revue bibliographique à la production de recommandations de gestion en passant par l’application de modèles spécifiques.

Listes de références publiées par des membres de SCIMABIO Interface

Un certain nombre de travaux utilisant les statistiques Bayésiennes dans différents cadres ont été publiés dans des revues scientifiques à comité de lecture par les collaborateurs de SCIMABIO Interface. Vous en trouverez ici une liste non-exhaustive.

  • Bouchard, C., and D. Nicolas. 2023. Estimating Migration Speed of Glass Eels during Their Colonization of a Mediterranean Lagoon. Journal of Fish Biology, August, jfb.15514. https://doi.org/10.1111/jfb.15514.
  • Bouchard, Colin, Cameron Bracken, Willy Dabin, Olivier Van Canneyt, Vincent Ridoux, Jérôme Spitz, and Matthieu Authier. 2019. A Risk-Based Forecast of Extreme Mortality Events in Small Cetaceans: Using Stranding Data to Inform Conservation Practice. Conservation Letters 12 (4): e12639. https://doi.org/10.1111/conl.12639.
  • Bouchard, C., Bardonnet, A., Buoro, M. and Tentelier, C. 2018. Effects of spatial aggregation of nests on population recruitment : the case of a small population of Atlantic salmon. – Ecosphere 9(4).
  • Bouchard, C., Buoro, M., Lebot, C. and Carlson, S. M. 2022a. Synchrony in population dyamics of juvenile Atlantic salmon : analyzing spatiotemporal variation and the influence of river flow and demography. – Canadian Journal of Fisheries and Aquatic Sciences 79(5) : 782–794.
  • Bouchard, C., Drouineau, H., Lambert, P., Boutron, O. and Nicolas, D. 2022b. Spatio-temporal variations in glass eel recruitment at the entrance pathways of a Mediterranean delta. – ICES Journal of Marine Science 79 : 1874–1887.
  • Vallecillo, D., Guillemain, M., Authier, M., Bouchard, C., Cohez, D., Vialet, E., Massez, G. et al. 2022. Accounting for detection probability with overestimation by integrating double monitoring programs over 40 years. – PLOS ONE 17(3) : e0265730.
  • Vallecillo, D., Guillemain, M., Bouchard, C., Roques, S. and Champagnon, J. 2023. Influence of changes in local environmental variables on the distribution and abundance dynamics of wintering Teal Anas crecca. – Biodiversity and Conservation .